Marketing mix modelling is an effective method to identify the main drivers of modelled variable and to explain how they contributed to its variation. The built models help understand the interactions among individual factors and the magnitude of their effect on the modelled variable.

In addition, the objective of marketing mix modelling has been shifting to the area of optimisations. The models are expected to lead to actionable recommendations on how to make marketing activities more effective and increase their return on investment (ROI).
The recommendations range from detailed insights into optimal spot duration, most suitable time of the day to advertise, better-working creatives and types of online display. They include optimisation of the budget split across media channels, distribution channels and geographical markets. And they enable to big picture scenarios of how much impact can be achieved with different budget levels.
Response Curve-Based Budget Split Optimisation
One way to go about split optimisations is to use response curves These are, in nutshell, S-shaped or logarithmic functions which graphically depict the response of sales, revenues or other modelled KPIs to increasing stimulus, such us media exposure. The response curves can be constructed at different levels of granularity for individual media channels, geographical regions or overall media spend.
They are factored into the procedure where the optimisation algorithm splits the available budget across media channels or geographical regions, based on their marginal return of additional $ invested.
For illustration, we use the results of market mix model to come up with ROI-maximizing budget split across media channels.
Response Curves Built From Aggregate Results of Historical Activities
One approach is to plot aggregate results for several past periods against their spend; and to construct the response curve which fits best the tested levels.

This approach is suitable for those channels where the marketer tested a wider range of spend levels, the scope of media activities was stable higher spend levels hit diminishing returns.
The analysis can provide inaccurate recommendations if the conditions above are not met.
First, if only a small range of spend levels were tested in the past, there is uncertainty, what the effect will be if the actual spend largely differs from the tested levels. This scenario is illustrated in chart above.

More specifically, if lower tested spend in past periods have not shown so far signs of diminishing returns (see figure on the right), there can be many scenarios how the effect develops in the upper parts of the response curve.
The optimised channel split is then affected by modeller’s expectations of how the response curve will behave at higher spend levels.
Second, simple annual or campaign response curves are disconnected from fligting. In other words, they do not take into account how media exposure to a particular channel was planned over the time and do not account for the possibility that different media planning can generate different results at the same level of spend. As such, the response curves do not provide guidelines for media flighting.
Third, response curves are often represented as projected revenues or volumes against spend. But one often uses other metrics than spend to model the impact of media. These are GRPs for TV or impressions for online display. If the price of a unit of media exposure increases – one can buy fewer units, i.e. GRPs or impressions, for the same budget. As a result, the recommended spend level might not deliver the volume uplift in line with the response curve projection.
How to go about these challenges? Use all the information in the model. Complex models should be used to their full potential to provide insights and projected outcomes of planned activities.
Response curves built from within-the-model simulated scenarios
This can be done through running scenarios directly within the existing model, simulating raised and decreased media exposure based on used media flighting. There are several good reasons for doing this;
First, the model, depending on the modelling approach, contains the information about channel performance, e.g. diminishing returns at weekly and overall burst level, memory effects, different performance of campaign, creative wear-out effects. The model incorporates them into the projected response.
Second, the response curves enables to see the impact of flighting on the overall media effect. In other words, such response curves help to assess how different flighting can result in a different response. Even more importantly, they also provide guidelines how to optimally plan media at different budget constraints. (See Case Study and accompanying two figures below).
Different Flighting Resulting in Different Response
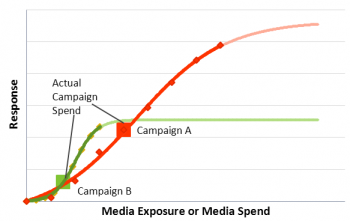
Brand ran two campaigns A and B in two consecutive periods, with Campaign A costing around 2.6 times more than campaign B. Flighting differed significantly, with Campaign A having a strong first burst continued by short bursts over 20 week period. Campaign B had much lower budget, with denser flighting over 9-week period.Simulating different levels of spend for the same flighting; we generated response curves for both campaigns. The results indicate that while for low budget levels, campaign B flighting provides better response, more continuous flighting of campaign A will generate better response for higher budgets. In both cases, if the budget exceeds twice of the actual tested level – uncertainty of the result is indicated through a lighter line. Also, the results imply that both campaigns, in particular Campaign B, could well absorb higher spend.
FLighting of two TV Campaigns and their
different response
Response curves for two campaigns 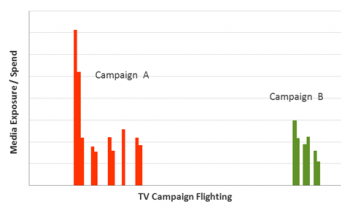
Third, a scenario planner automatically takes into account all changes in media prices and adjusts the optimal budget split accordingly.
Fourth, the modelled sales are driven by other factors in addition to media communications. These include other elements of marketing mix, such as price and distribution, as well as a range of external factors. One can run scenarios with different levels of channel spend, keeping the rest of the model intact. As such the built response curves are better representations of how the media channel would perform at different levels of spend.
Challenge of Predictions That Are Far From the Tested Levels
One of the issues mentioned above – uncertainty of the response when the planned spend is significantly above or below the tested levels – cannot be fully resolved through the suggested approach. In this respect, one needs to undertake tests at higher spend levels to get further insights.
If diminishing returns have not been hit so far due to a low spend, the optimisation algorithm might recommend a strong increase in spend on the back of a (close to linear) response curve and the expected big volume uplift. However, this response pattern is unlikely to hold as the channel budget increases. The modeller therefore needs to introduce an element of risk management and constrain spend at own discretion. Departing from the past levels, the maximum recommended spend depends on the budget size and risk-aversion of a media planner or marketer.
To Sum Up
Given increasing importance of mix models for media planning, it is essential to use them to their full potential for projections and optimisations. The suggested approach to building response curves within the model provides more accurate projection of expected media effect and a stronger base for budget split optimisation.
Last but not least, a more detailed look into the nature of media impact can also serve as a starting point for discussions between the client and analysts about the media performance under a wide range of market scenarios and their implications for media planning.
Sydney, 05 April 2013,
Elena Yusupova, PhD
